It's Actors All The Way Down

Some language environments provide an interactive interface called a Read-Eval-Print-Loop (abbreviated REPL). One key characteristic of a REPL is the ability to incrementally define, extend and re-define your environment. This is particularly challenging in a pure-functional context, such as the evaluator we have developed so far. Modularity and incremental development seems to imply the need for an environment with “history”, thus introducing shared mutable state [1].

As it turns out, solutions to the problem of incremental definition also address the problem of mutually recursive references. Of course it is well-known that recursive functions can be defined through the use of a Recursive Fixed Point Combinator (or Y-Combinator) [2], however extending this technique to multiple mutually-recursive definitions can be quite difficult. It is more practical, and easier to understand, if we resolve mutually recursive references via the dreaded “shared mutable state”. In our case, this will take the form of a dynamic “top-level” environment.

In part 4 we introduced the LET/IN expression. This allowed us to extend our lexical environment with new bindings, and then evaluate an expression in the extended environment. However, the equation portion of the LET is still evaluated in the original environment. This means that we cannot make reference in the equation to identifiers bound by the equation. For example:

LET reverse = \list.(
	CASE list OF
	(h, t) : (reverse(t), h)  # <-- ERROR: reverse is undefined here!
	_ : (list)
	END
) IN reverse(1, 2, 3)

In order to support incremental definition, as well as allow for mutually recursive references, we introduce the statement form of LET.

repl  ::= <stmt>+;
stmt  ::= 'LET' <eqtn>
        | <expr>;

Our definition of expr, and the rest of the grammar, remains the same as in part 4. We’ve simply added a new “top-level” production repl consisting of a sequence of statements. Each statement is either a LET statement, or an expression (including LET/IN). The “value” of each statement is printed to the interactive console. If we enter the code

LET reverse = \list.(
	CASE list OF
	(h, t) : (reverse(t), h)
	_ : (list)
	END
)

reverse(1, 2, 3)

at the interactive console, we would see

#ok
3, 2, 1

printed in response.

LET statement

Statements respond to #exec requests, rather than the #eval requests that drive expressions. The LET statement attempts to unify an equation, potentially adding bindings to the (mutable) environment.

LET let_stmt_beh(eqtn) = \(cust, #exec, env).[
	SEND (k_env, #unify, env) TO eqtn
	CREATE k_env WITH \env'.[
		CASE env' OF
		? : [ SEND #fail TO cust ]
		_ : [ SEND #ok TO cust ]
		END
	]
]

When let_stmt_beh receives an #exec request, it sends a #unify request to its equation eqtn. The customer for this request k_env receives the environment env’ resulting from the unification. If this environment is undefined, then #fail is sent to the customer. Otherwise #ok is sent, signaling successful completion of the statement.

Notice that we throw away the “extended” environment env’ on success. This is because we have changed our assumptions about the original environment env. We now assume that bindings are accomplished (via the identifier pattern) using a side-effect on the environment, rather than creating a new extended environment.

Identifier pattern

The identifier pattern has been responsible for creating an extended environment to capture the binding of the identifier to a value. Now we want to delegate the binding responsibility to the environment itself.

LET ident_ptrn_beh(ident) = \(cust, req).[
	CASE req OF
	(#match, value, env) : [
		SEND (cust, #bind, ident, value) TO env
	]
	(#eq, right, env) : [
		SEND (cust, #bind, SELF, env) TO right
	]
	(#pair, pair, env) : [
		SEND (cust, #bind, SELF, env) TO pair
	]
	_ : [ SEND ? TO cust ]
	END
]

When ident_ptrn_beh receives a #match request, it sends a #bind request to the environment. The environment will respond to the customer with the “extended” environment.

Dynamic Environment

The environment passed to a statement in an #exec message must be a mutable environment. This environment must understand the #bind messages it receives from identifier patterns, and modify itself to establish new equalities.

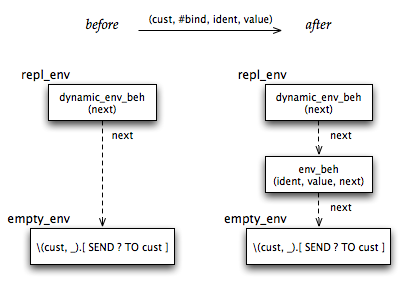
CREATE empty_env WITH \(cust, _).[ SEND ? TO cust ]  # ...from part 1

CREATE repl_env WITH dynamic_env_beh(empty_env)

LET dynamic_env_beh(next) = \(cust, req).[
	CASE req OF
	(#bind, ident, value) : [
		CREATE next' WITH env_beh(ident, value, next)
		BECOME dynamic_env_beh(next')
		SEND SELF TO cust
	]
	_ : [ SEND (cust, req) TO next ]
	END
]

The “top-level” environment for the REPL repl_env has dynamic_env_beh and delegates to the empty environment empty_env (from part 1). When statements are executed, repl_env is provided as the environment in the #exec request.

When dynamic_env_beh receives a #bind message, it creates a new environment binding next’ and updates its next to become next’. The new binding delegates to the original next. In effect, this inserts a new binding after the dynamic environment, as shown in Figure 1. Finally, the dynamic environment sends its SELF (as the “extended” environment) to the customer cust.

Figure 1 - Extending a Dynamic Environment

Bound Environment

Bindings added to the dynamic environment become the immutable lexically-scoped environment. Bindings are never changed, but may be superseded by newer bindings. Since we added the #bind message to the environment’s protocol, it seems prudent to clarify the intent of messages that retrieve the values of bound variables. Previously, it was enough to simply give the identifier and a customer for the value. Now we add the symbol #lookup to the message.

LET env_beh(ident, value, next) = \(cust, req).[
	CASE req OF
	(#lookup, $ident) : [ SEND value TO cust ]
	_ : [ SEND (cust, req) TO next ]
	END
]

Of course, this requires a corresponding change in identifier expressions. Since they retrieve values bound to identifiers in the environment, they need to use the new form of #lookup message.

LET ident_expr_beh(ident) = \(cust, #eval, env).[
	SEND (cust, #lookup, ident) TO env
]

Finally, we consider the required modifications to closures and conditional expressions. Since equation unification no longer adds bindings directly to the environment, we must use our new dynamic environment to capture the bindings created during pattern matching.

LET ptrn_closure_beh(ptrn, body, env) = \(cust, #apply, arg).[
	CREATE env' WITH dynamic_env_beh(env)
	SEND (k_env, #match, arg, env') TO ptrn
	CREATE k_env WITH \env'.[
		CASE env' OF
		? : [ SEND ? TO cust ]
		_ : [ SEND (cust, #eval, env') TO body ]
		END
	]
]

The CASE expression and IF expression require similar changes.

LET case_choice_beh(ptrn, expr, next) = \(cust, #match, value, env).[
	CREATE env' WITH dynamic_env_beh(env)
	SEND (k_match, #match, value, env') TO ptrn
	CREATE k_match WITH \env'.[
		CASE env' OF
		? : [ SEND (cust, #match, value, env) TO next ]
		_ : [ SEND (cust, #eval, env') TO expr ]
		END
	]
]
LET if_expr_beh(eqtn, expr, else) = \(cust, #eval, env).[
	CREATE env' WITH dynamic_env_beh(env)
	SEND (k_env, #unify, env') TO eqtn
	CREATE k_env WITH \env'.[
		CASE env' OF
		? : [ SEND (cust, #eval, env) TO else ]
		_ : [ SEND (cust, #eval, env') TO expr ]
		END
	]
]

If matching/unification fails, we revert to the original environment, without the dynamic environment extension.

Odd/Even Example

A classic example of mutual recursion is an odd/even test for positive integers. Although this algorithm is quite inefficient, it is easy to understand and clearly requires mutual recursion. For these definitions to work, we need a way to resolve the mutual references. Our shared mutable environment accomplishes this.

LET even? = \n.(
	CASE n OF
	0 : TRUE
	_ : odd?(dec(n))
	END
)
#ok

LET odd? = \n.(
	CASE n OF
	0 : FALSE
	_ : even?(dec(n))
	END
)
#ok

even?(3)
FALSE

odd?(3)
TRUE

This example assumes an environment where dec is bound to an integer decrement function. The two LET statements establish definitions for even? and odd? functions. Each function contains a reference to the other. Both are “closed” in the dynamic “top-level” environment, so both have access to all top-level definitions, including their own, regardless of when they are added. In fact, it is possible to re-define dec and the “new” definition would be used for subsequent evaluations of even? and odd?.

Summary

In this part of our series implementing programming language constructs with actors, we introduce the LET statement, which operates on a shared mutable “top-level” environment. This provides the means to incrementally define, extend and re-define the environment. In addition, it allows for mutually recursive references in definitions.

The LET statement is the first imperative feature we have introduced to our language. In doing so, we have made a clear distinction between expressions, which represent immutable values, and statements, which represent imperatives that operate on shared mutable state. In part 6 we will continue to explore useful imperative statements.

References

[1]

G. Steele, G. Sussman. The Art of the Interpreter or, the Modularity Complex (Parts Zero, One, and Two). AIM-453, MIT, 1978.

[2]

R. Gabriel. The Why of Y. http://www.dreamsongs.com/Files/WhyOfY.pdf, 2001